Vrstjr

  本條目介紹的是磁性物質或電流產生的磁場。關於磁性物質顯示出的物理現象，請見“磁”。關於各種各樣的鐵磁性物質，請見“磁鐵”。

感受到在玻璃下方的磁鐵所產生的強烈磁場，在玻璃上方的鐵磁流體，會顯示出正常場不穩定性。

在電磁學裡，磁石、磁鐵、電流及含時電場，都會產生磁場^[1][2]:3-4。處於磁場中的磁性物質或電流，會因為磁場的作用而感受到磁力，因而顯示出磁場的存在。磁場是一種向量場；磁場在空間裡的任意位置都具有方向和數值大小^{[notes 1]}。

磁鐵與磁鐵之間，通過各自產生的磁場，互相施加作用力和力矩於對方。運動中的電荷亦會產生磁場。磁性物質產生的磁場可以用電荷運動模型來解釋^{[notes 2]}。

當施加外磁場於物質時，磁性物質的內部會被磁化，會出現很多微小的磁偶極子。磁化強度估量物質被磁化的程度。知道磁性物質的磁化強度，就可以計算出磁性物質本身產生的磁場。產生磁場需要輸入能量，當磁場被湮滅時，這能量可以再回收利用，因此，這能量被視為儲存於磁場。

電場是由電荷產生的。電場與磁場有密切的關係；含時磁場會生成電場，含時電場會生成磁場。馬克士威方程組描述電場、磁場、產生這些向量場的電流和電荷，這些物理量之間的詳細關係。根據狹義相對論，電場和磁場是電磁場的兩面。設定兩個參考系A和B，相對於參考系A，參考系B以有限速度移動。從參考系A觀察為靜止電荷產生的純電場，在參考系B觀察則成為移動中的電荷所產生的電場和磁場。

在量子力學裏，科學家認為，純磁場（和純電場）是虛光子所造成的效應。以標準模型的術語來表達，光子是所有電磁作用的顯現所依賴的媒介。對於大多數案例，不需要這樣微觀的描述，在本文章內陳述的簡單經典理論就足足有餘了；在低場能量狀況，其中的差別是可以忽略的。

在古今社會裡，很多對世界文明有重大貢獻的發明都涉及到磁場的概念。地球能夠產生自己的磁場，這在導航方面非常重要，因為指南針的指北極準確地指向位置在地球的地理北極附近的地磁北極。電動機和發電機的運作機制是倚賴磁鐵轉動使得磁場隨著時間而改變。通過霍爾效應，可以給出物質的帶電粒子的性質。磁路學專門研討，各種各樣像變壓器一類的電子元件，其內部磁場的相互作用。

定義

按照磁場對於周圍環境的影響，可以用幾種等價的方法來定義磁場。例如，類似於電場，磁場對電荷會施加作用力；但與電場不同的是，它只對移動中的電荷施加作用力，而且作用力的方向垂直於磁場本身和電荷速度。這作用力稱為勞侖茲力，以方程式表示，

F=qv×B{displaystyle mathbf {F} =qmathbf {v} times mathbf {B} }；

其中，

F{displaystyle mathbf {F} }是作用力，以牛頓為測量單位，

q{displaystyle q}是電荷量，以庫侖為測量單位，

v{displaystyle mathbf {v} }是電荷q{displaystyle q}的速度，以公尺／秒為測量單位。

另外一種對於磁場的工作定義是由處於磁場的磁偶極子所感受到的力矩給出，以方程式表示，

τ=μ×B{displaystyle {boldsymbol {tau }}={boldsymbol {mu }}times mathbf {B} }；

其中，

τ{displaystyle {boldsymbol {tau }}}是力矩，以牛頓·公尺為測量單位，

μ{displaystyle {boldsymbol {mu }}}是磁偶極子的磁偶極矩，以公尺²·安培為測量單位。

歷史

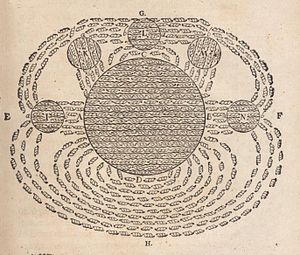
最早出現的幾副磁場繪圖之一，繪者為勒內·笛卡兒，1644年。這繪圖顯示出地球（中心大圓球）的磁場吸引幾塊圓形磁石（以I、K、L、M、N標記的圓球)。笛卡兒認為磁性是由微小螺旋狀粒子的環流造成的，稱為「螺紋子」。這些螺紋子穿過磁鐵的平行螺紋細孔，從指南極（A）進入，從指北極（B）出來，經過磁鐵外的空間（G、H）再繞回指南極。當螺紋子繞動至磁石附近時，會穿過其細孔，從而造成磁力。

雖然很早以前，人類就已知道磁石和其奧妙的磁性，最早出現的幾個學術性論述之一，是由法國學者皮埃·德馬立克（Pierre de Maricourt）於公元1269年寫成^{[notes 3]}。德馬立克仔細標明了鐵針在塊型磁石附近各個位置的定向，從這些記號，又描繪出很多條磁場線。他發現這些磁場線相會於磁石的相反兩端位置，就好像地球的經線相會於南極與北極。因此，他稱這兩位置為磁極^[3]。幾乎三個世紀後，威廉·吉爾伯特主張地球本身就是一個大磁石，其兩個磁極分別位於南極與北極。出版於1600年，吉爾伯特的巨著《論磁石》（De Magnete）開創磁學為一門正統科學學術領域。

於1824年，西莫恩·帕松發展出一種物理模型，比較能夠描述磁場。帕松認為磁性是由磁荷產生的，同類磁荷相排斥，異類磁荷相吸引。他的模型完全類比現代靜電模型；磁荷產生磁場，就如同電荷產生電場一般。這理論甚至能夠正確地預測儲存於磁場的能量^{[notes 4]}。

儘管帕松模型有其成功之處^{[notes 5]}，這模型也有兩點嚴峻瑕疵。第一，磁荷並不存在。將磁鐵切為兩半，並不會造成兩個分離的磁極，所得到的兩個分離的磁鐵，每一個都有自己的指南極和指北極。第二，這模型不能解釋電場與磁場之間的奇異關係。

於1820年，一系列的革命性發現，促使開啟了現代磁學理論。首先，丹麥物理學家漢斯·奧斯特於7月發現載流導線的電流會施加作用力於磁針，使磁針偏轉指向。稍後，於9月，在這新聞抵達法國科學院僅僅一周之後，安德烈-瑪麗·安培成功地做實驗展示出，假若所載電流的流向相同，則兩條平行的載流導線會互相吸引；否則，假若流向相反，則會互相排斥。緊接著，法國物理學家讓-巴蒂斯特·必歐和菲利克斯·沙伐於10月共同發表了必歐-沙伐定律；這定律能夠正確地計算出在載流導線四周的磁場。

1825年，安培又發表了安培定律。這定律也能夠描述載流導線產生的磁場。更重要的，這定律幫助建立整個電磁理論的基礎。於1831年，麥可·法拉第證實，隨著時間而變化的磁場會生成電場。這實驗結果展示出電與磁之間更密切的關係。

從1861年到1865之間，詹姆斯·馬克士威將經典電學和磁學雜亂無章的方程式加以整合，發展成功馬克士威方程組。最先發表於他的1861年論文《論物理力線》，這方程組能夠解釋經典電學和磁學的各種現象。在論文裡，他提出了「分子渦流模型」，並成功地將安培定律加以延伸，增加入了一個有關於位移電流的項目，稱為「馬克士威修正項」。由於分子渦包具有彈性，這模型可以描述電磁波的物理行為。因此，馬克士威推導出電磁波方程式。他又計算出電磁波的傳播速度，發現這數值與光速非常接近。警覺的馬克士威立刻斷定光波就是一種電磁波。後來，於1887年，海因里希·赫茲做實驗證明了這事實。馬克士威統一了電學、磁學、光學理論。

雖然，有了極具功能的馬克士威方程組，經典電動力學基本上已經完備，在理論方面，二十世紀帶來了更多的改良與延伸。阿爾伯特·愛因斯坦，於1905年，在他的論文裡表明，電場和磁場是處於不同參考系的觀察者所觀察到的同樣現象（幫助愛因斯坦發展出狹義相對論的思想實驗，關於其詳盡細節，請參閱移動中的磁鐵與導體問題）。後來，電動力學又與量子力學合併為量子電動力學。

B場與H場

在各個學術領域裡，磁場會被用來稱呼兩種不同的向量場，分別標記為H{displaystyle mathbf {H} }和B{displaystyle mathbf {B} }。向量場H{displaystyle mathbf {H} }又時常稱為「磁場強度」（magnetic field intensity或magnetic field strength）或「附屬磁場」（auxiliary magnetic field）或乾脆「H場」^[4]。向量場B{displaystyle mathbf {B} }也時常稱為「磁通量密度」（magnetic flux density）、「磁感應强度」（magnetic induction）、「B場」。

雖然「磁場」這個詞彙在歷史上已先被H場占有，而只能將B場稱為「磁感應」，但是現在多數物理學家公認B場為更基本的物理量，因此他們稱呼B場為「磁場」^{[notes 6]}。如同命名表格展示，B場和H場的習慣命名並不一致。為了分歧義，在本文章裏，磁感應強度指的是B場，磁場強度指的是H場，而磁場則依上下文而定，通常指的是B場。

H場以方程式定義為^[5]

H =def Bμ0−M{displaystyle mathbf {H} {stackrel {def}{=}} {frac {mathbf {B} }{mu _{0}}}-mathbf {M} }；

其中，μ0{displaystyle mu _{0}}是磁常數，M{displaystyle mathbf {M} }是磁化強度。

對於線性物質，磁化強度M{displaystyle mathbf {M} }與B場成正比，所以，B場與H場之間的關係為

H=Bμ′{displaystyle mathbf {H} ={frac {mathbf {B} }{mu '}}}；

其中，μ′{displaystyle mu '}是磁導率。

在自由空間裏，磁化強度等於零，所以，

H=Bμ0{displaystyle mathbf {H} ={frac {mathbf {B} }{mu _{0}}}}。

對於很多其它物質，磁化強度與B場之間的關係相當複雜。例如，鐵磁性物質和超導體的磁化強度是B{displaystyle mathbf {B} }的多值函數（multivalued function）。這現象稱為遲滯現象^[6]。

在國際單位制裡，B場的單位為特斯拉（tesla），等價於韋伯（weber）／平方米，或伏特·秒／平方米。在CGS單位制裡，B場的單位為高斯（gauss）。1特斯拉等於10,000高斯。在國際單位制裡，H場的單位為安培／公尺；在CGS單位制裡，H場的單位為奧斯特（oersted）。1奧斯特定義為1000/4π≈79.5774715{displaystyle 1000/4pi approx 79.5774715}安培／公尺^[7]。

精密儀器能夠測量到的最微小磁場的數量級為阿托特斯拉（10⁻¹⁸特斯拉）^[8]；實驗室能夠製備的最強烈磁場為2800特斯拉^[9]。很多像磁星一類的天文星體，其磁場值域為0.1至100吉咖特斯拉（10⁸至10¹¹特斯拉），超強於最強烈的實驗室磁場^[10]。

磁強計（magnetometer）是測量局域磁場的儀器。磁強計又分為很多類，重要的幾類包括霍爾效應磁強計、超導磁強計、核子旋進磁力儀（NMR magnetometer）、磁通門磁強計（fluxgate magnetometer）等等。遙遠的天文星體的磁場可以靠著測量其對於附近帶電粒子的影響而得知。例如，繞著磁場線螺旋轉動的電子會產生同步輻射，其無線電波數據可以用電波望遠鏡偵測獲得。

磁場線

透過鐵粉顯示出的磁場線。

磁場的方向可以藉著磁偶極子的性質來顯示，處於磁場的磁偶極子會沿著磁場的磁場線平行排列，其中的一個顯著例子就是磁鐵周圍的鐵粉分佈圖案。將條狀磁鐵放在白紙下面，鋪灑一堆鐵粉在白紙上面，這些鐵粉會依著正切磁場線的方向排列，形成一條條曲線，在曲線的每一點顯示出磁場線的正切方向。這曲線圖稱為「場線圖」。

繪製場線圖是一種很簡單的、描述磁場（或任意其它向量場）的方法，在空間的任意位置的磁場可以從場線圖在對應位置的場線正切方向和密度估計出來。磁場線密度越高表示磁場越強勁。場線圖的繪製相當容易。首先，在每一個位置測量磁場的數值大小和方向。按照所得數據，在圖紙的對應位置繪出一條跟磁場同方向的箭桿。然後，將每條箭桿之首部與前面的箭桿之尾部連接起來，形成磁場線，確使磁場線密度與磁場的強度成正比。這樣，就可以繪製出一幅場線圖。這是一種很優良的磁場視覺化方法。想像磁場線會沿著線徑施加張力（像一條橡皮圈），又會垂直於線徑對鄰近的磁場線施加壓力，這就是磁力的物理行為。兩塊磁鐵的異性磁極互相吸引，這是由於它們被很多條磁場線連結；反之，兩塊磁鐵的同性磁極互相排斥，這是由於它們的磁場線不相交接，因為互相平行，造成互相推擠。

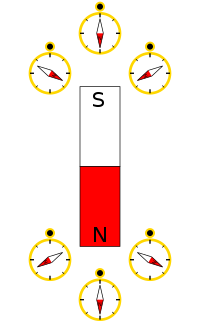
指南針顯示出一個條形磁鐵的磁場方向。指南針的指北極（紅色）會被磁鐵的指南極（S極）吸引，也會被磁鐵的指北極（N極）排斥。

磁場在任意位置的方向可以用指南針來顯示。指南針可以顯示出一個條形磁鐵的磁場方向。由於異性磁極相互吸引，指南針的指北極會被磁鐵的指南極（S極）吸引；由於同性磁極相互排斥，指南針的指北極會被磁鐵的指北極（N極）排斥。在磁鐵的指南極附近，磁場指向磁鐵；在指北極附近，磁場背向磁鐵。載流導線產生的磁場不會指向導線，也不會背向導線，而會環繞著導線。

出現於地球北極高空或南極高空的極光也可以顯示出磁場線。從太陽流出來的大量離子形成了太陽風，其中一部分會流往地球，在地球高空，被地球磁場捕獲，沿著磁場線集中至北極高空與南極高空。這些離子跟大氣層的原子、分子之間的碰撞，造成了能量以極光形式被釋出。通常，極光看起來像是漫射（diffusion）的輝光（glow）或「光簾」，朝著東-西方向延伸。每一張光簾是由許多條平行射線組成。每一條射線與在那位置的磁場線同方向。這令人覺得極光是由地球的磁場塑造成形的。確實無誤，從人造衛星的觀察證實了離子被磁場線引導，一邊繞著磁場線盤旋，一邊朝著地球移動。

磁场散度为0

繪製場線圖是一種很有用的表示向量場的方法，可以很簡單地顯示出向量場的細緻屬性。磁場的一個很重要的性質可以用場線圖顯示出來：磁場線沒有初始點，也沒有終結點；磁場線會形成閉迴路，或從無窮遠延伸至無窮遠。至今，科學家尚未發現任何例外。磁場是一種螺線向量場。

磁場線會從磁鐵的指北極附近離開磁鐵，又會從磁鐵的指南極附近進入磁鐵；在磁鐵內部，磁場線仍舊從指南極連結至指北極^{[notes 7]}。任何一條進入磁鐵的磁場線必定會從磁鐵出來；絕不容許磁場線終結於任何位置。磁極總是以指北極和指南極一對一對的形式出現。將磁鐵切為兩半，會形成兩塊磁鐵，其中每一塊磁鐵都擁有自己的指北極和指南極。

更正式而言，所有進入某區域的磁場線，也必須離開那區域。因此，進入某區域的磁場線的數目^{[notes 8]}，減去離開那區域的磁場線的數目，結果必須等於零。這結果稱為高斯磁定律，以方程式表示：

∮S⁡B⋅da=0{displaystyle oint _{mathbb {S} }mathbf {B} cdot mathrm {d} mathbf {a} =0}；

其中，S{displaystyle mathbb {S} }是閉曲面，da{displaystyle mathrm {d} mathbf {a} }是微小面元素。

H場線開始與終結於磁極

在磁性物質外面，H場線與B場線等同；但在磁性物質內部，H場與B場的數值大小、方向可能不同，這依賴磁化強度M{displaystyle mathbf {M} }而定，這關係可以由H場的定義方程式看出來：

H =def Bμ0−M{displaystyle mathbf {H} {stackrel {def}{=}} {frac {mathbf {B} }{mu _{0}}}-mathbf {M} }。

假設外磁場等於零，則在一個均勻磁鐵內部，B場與H場呈相反方向。H場線開始於指北極，終結於指南極。相與比較，B場線形成一個閉迴圈，在磁鐵內部，從指南極延續到指北極，在磁鐵外部，又從指北極繞道至指南極。H場線與電場線類似；電場線開始於正電荷，終結於負電荷。這使人想要以處於兩端局域的磁荷為磁鐵的模型。很可惜地，這磁荷模型並不正確，尤其是當計算磁鐵內部的磁場時。

一個磁化強度為M=Mz^{displaystyle mathbf {M} =M{hat {z}}}的均勻磁性球體。

例如，參閱右圖，採用原子尺寸載流迴圈模型來描述，一個磁化強度為M=Mz^{displaystyle mathbf {M} =M{hat {z}}}均勻磁性球體，等價於一個滿足以下條件的球體：內部的束縛電流密度Jb{displaystyle J_{b}}和表面束縛電流密度Kb{displaystyle K_{b}}分別為

Jb =def ∇×M=0{displaystyle J_{b} {stackrel {def}{=}} nabla times mathbf {M} ={boldsymbol {0}}}、

Kb =def M×n^=Msin⁡θ{displaystyle K_{b} {stackrel {def}{=}} mathbf {M} times {hat {n}}=Msin theta }；

其中，n^{displaystyle {hat {n}}}是垂直於球體表面的徑向單位向量。

經過一番運算，可以得到，表面束縛電流密度為Msin⁡θ{displaystyle Msin theta }的球體，其內部B場為

B=z^2μ0M/3{displaystyle mathbf {B} ={hat {z}}2mu _{0}M/3}。

從H場H{displaystyle mathbf {H} }的定義式，

H=−z^M/3{displaystyle mathbf {H} =-{hat {z}}M/3}。

所以，在均勻磁化球體內部，B場與H場呈相反方向^[11]。

磁單極子

磁單極子是一種假想的粒子（或粒子類），這粒子只擁有一個磁極（指北極或指南極）。換句話說，類似帶電粒子的擁有電荷，磁單極子擁有磁荷。

現今，對於這概念的興趣大多出自於粒子物理學，特別值得注意的是大統一理論和超弦理論，關於磁單極子的存在或可能性，它們做了很多預測，因而激發出許多物理學者尋找磁單極子的強烈興趣。但儘管竭盡全力，物理學者至今仍舊無法觀察到任何磁單極子的蛛絲馬跡^{[notes 9]}

最新進研究發現自旋冰（spin ice）是一種可以模擬磁單極子的材料，但不含有真實的磁單極子。

磁偶極子

假設一個平面載流迴圈的面積向量為a{displaystyle mathbf {a} }、所載電流為I{displaystyle I}，則其磁偶極矩為μ=Ia{displaystyle {boldsymbol {mu }}=Imathbf {a} }。

假設一個平面載流迴圈的面積向量為a{displaystyle mathbf {a} }、所載電流為I{displaystyle I}，則其磁偶極矩μ{displaystyle {boldsymbol {mu }}}的方向，根據右手法則，是大拇指從載流迴圈的平面指出的方向，而其它拇指的指向則與電流的流動方向相同，磁偶極矩的大小等於電流乘以迴圈的面積。以方程式表示，磁偶極矩μ{displaystyle {boldsymbol {mu }}}為

μ=Ia{displaystyle {boldsymbol {mu }}=Imathbf {a} }。

這有限面積的載流迴圈還有更高階的磁矩，像磁四極矩，磁八極矩等等。假設載流迴圈的面積趨向於零、電流趨向於無窮大，同時保持μ=Ia{displaystyle {boldsymbol {mu }}=Imathbf {a} }不變，則所有更高階的磁矩會趨向於零，這真實的載流迴圈趨向於一個理想磁偶極子，或純磁偶極子。這模型稱為電流模型。採用這模型，可以很容易地找到角動量與磁矩之間的關係。愛因斯坦－德哈斯效應，由磁化而產生的旋轉現象，和其逆反，巴尼特效應（Barnett effect），由旋轉而產生的磁化現象，這兩種效應基本是在展示角動量與磁矩之間的關係。應用巴尼特效應，將載流迴圈順著電流方向旋轉，會使電流增大，連帶地也增大了磁矩。

磁偶極子的磁場

一個指向右方的磁偶極子的磁場線。

假設磁偶極矩為μ{displaystyle {boldsymbol {mu }}}的磁偶極子，其位置是在原點，則在任意位置r{displaystyle mathbf {r} }，磁偶極子的向量勢A{displaystyle mathbf {A} }是

A(r)=μ04πr2(μ×r^){displaystyle mathbf {A} (mathbf {r} )={frac {mu _{0}}{4pi r^{2}}}({boldsymbol {mu }}times {hat {mathbf {r} }})}；

其中，μ0{displaystyle mu _{0}}是磁常數。

這磁偶極子所產生的磁場B{displaystyle mathbf {B} }為

B=∇×A{displaystyle mathbf {B} =nabla times mathbf {A} }。

由於磁偶極子的向量勢有一個奇點在它所處的位置（原點O{displaystyle mathbf {O} }），必須特別小心地計算，才能得到正確答案。更仔細地推導，可以得到磁場為

B(r)=μ04πr3(3(μ⋅r^)r^−μ)+2μ0μ3δ3(r){displaystyle mathbf {B} (mathbf {r} )={frac {mu _{0}}{4pi r^{3}}}left(3({boldsymbol {mu }}cdot {hat {mathbf {r} }}){hat {mathbf {r} }}-{boldsymbol {mu }}right)+{frac {2mu _{0}{boldsymbol {mu }}}{3}}delta ^{3}(mathbf {r} )}。

任意磁場的多極展開式中，帶頭項目就是這公式右手邊的第一個項目，偶極子項目。磁場沒有單極子項目。在遠距離，這公式近似任何類似磁偶極子的組態所產生的磁場。

磁偶極子感受到的磁力矩

處於均勻磁場的一個方形載流迴圈。

如圖右，假設載有電流I{displaystyle I}的一個方形迴圈處於外磁場B=B0z^{displaystyle mathbf {B} =B_{0}{hat {mathbf {z} }}}。方形迴圈四個邊的邊長為w{displaystyle w}，其中兩個與y^{displaystyle {hat {mathbf {y} }}}平行的邊垂直於外磁場，另外兩個邊與磁場之間的夾角角弧為−θ+π/2{displaystyle -theta +pi /2}。

垂直於外磁場的兩個邊所感受的磁力矩為

τ=(IwB0wsin⁡θ2+IwB0wsin⁡θ2)y^=Iw2B0sin⁡θy^{displaystyle {boldsymbol {tau }}=left(IwB_{0}{frac {wsin {theta }}{2}}+IwB_{0}{frac {wsin {theta }}{2}}right){hat {mathbf {y} }}=Iw^{2}B_{0}sin {theta }{hat {mathbf {y} }}}。

另外兩個邊所感受的磁力矩互相抵消。注意到這迴圈的磁偶極矩為 μ=Iw2μ^{displaystyle {boldsymbol {mu }}=Iw^{2}{hat {boldsymbol {mu }}}}。所以，這迴圈感受到的磁力矩為

τ=μ×B{displaystyle {boldsymbol {tau }}={boldsymbol {mu }}times mathbf {B} }。

令載流迴圈的面積趨向於零、電流趨向於無窮大，同時保持μ=Ia{displaystyle {boldsymbol {mu }}=Imathbf {a} }不變，則這載流迴圈趨向於理想磁偶極子。所以，處於外磁場的磁偶極子所感受到的磁力矩也可以用上述方程式表示。

當磁偶極矩垂直於磁場時，磁力矩的大小是最大值μB0{displaystyle mu B_{0}}；當磁偶極矩與磁場同線時，磁力矩等於零。

磁偶極子的勢能

將載流迴圈從角弧θ1{displaystyle theta _{1}}扭轉到角弧θ2{displaystyle theta _{2}}，磁場所做的機械功W{displaystyle W}為

W=−∫θ1θ2τ dθ=−∫θ1θ2μB0sin⁡θ dθ=μB0(cos⁡θ2−cos⁡θ1){displaystyle W=-int _{theta _{1}}^{theta _{2}}tau mathrm {d} theta =-int _{theta _{1}}^{theta _{2}}mu B_{0}sin {theta } mathrm {d} theta =mu B_{0}(cos {theta _{2}}-cos {theta _{1}})}。

注意到磁力矩的扭轉方向是反時針方向，而θ{displaystyle theta }是朝著順時針方向遞增，所以必須添加一個負號。設定θ1=π/2{displaystyle theta _{1}=pi /2}，則

W=μB0cos⁡θ2=μ⋅B{displaystyle W=mu B_{0}cos {theta _{2}}={boldsymbol {mu }}cdot mathbf {B} }。

對抗這磁場的磁力矩，將載流迴圈從角弧π/2{displaystyle pi /2}扭轉到角弧θ2{displaystyle theta _{2}}，所做的機械功Wa{displaystyle W_{a}}為

Wa=−W=−μ⋅B{displaystyle W_{a}=-W=-{boldsymbol {mu }}cdot mathbf {B} }。

定義載流迴圈的勢能U{displaystyle U}等於這機械功Wa{displaystyle W_{a}}，以方程式表示為

U=−μ⋅B{displaystyle U=-{boldsymbol {mu }}cdot mathbf {B} }。

這也是磁偶極子的勢能。當磁矩垂直於磁場時，勢能等於零；當磁矩與磁場呈相同方向時，勢能是最小值−μB0{displaystyle -mu B_{0}}；當磁矩與磁場呈相反方向時，勢能是最大值μB0{displaystyle mu B_{0}}。

永久磁鐵

永久磁鐵會在周圍產生持續不變的磁場。永久磁鐵大多是由像鐵或鎳一類的鐵磁性物質經過磁化而製成。每一個永久磁鐵都具有磁矩，其方向是從磁鐵的指南極指向指北極。指南極和指北極分別位於條形磁鐵的兩端，稱為「磁極」。

永久磁鐵的磁場

永久磁鐵的磁場比較複雜，特別是在磁鐵附近。一個微小條形磁鐵^{[notes 10]}的磁場與其磁矩成正比，也會與磁鐵的定向有關。當尺寸驅向無窮小極限時，磁鐵可以理想化成為磁偶極子，以方程式表示，這微小條形磁鐵（磁偶極子）產生的磁場為

B(r)=μ04πr3[3(μ⋅r^)r^−μ]{displaystyle mathbf {B} (mathbf {r} )={frac {mu _{0}}{4pi r^{3}}}left[3({boldsymbol {mu }}cdot {hat {mathbf {r} }}){hat {mathbf {r} }}-{boldsymbol {mu }}right]}；

其中，r{displaystyle mathbf {r} }是從磁鐵位置至場位置的位移向量，其單位向量是r^{displaystyle {hat {mathbf {r} }}}，其距離是r{displaystyle r}，μ0{displaystyle mu _{0}}是磁常數，μ{displaystyle {boldsymbol {mu }}}是微小磁鐵的磁矩。

有時候，磁鐵與磁鐵之間感受到的磁力和力矩，可以採用「磁極模型」來計算，磁極與磁極之間會互相吸引或互相排斥，就好像電荷與電荷之間的庫倫力。很可惜地，磁極模型不能正確地反映出磁鐵內部的真實狀況（請參閱鐵磁性）。科學家尚未找到磁荷存在的實證。磁鐵的指北極與指南極無法被分離；任何分離動作會造成兩個子磁鐵，各自擁有自己的指北極與指南極。磁極模型無法解釋電流產生的磁場，也無法解釋移動於磁場中的電荷所感受到的勞侖茲力。

更正確地描述磁性，涉及了計算廣泛分佈於磁鐵內部的原子尺寸載流迴圈所產生的磁場^[12]。

外磁場作用於磁鐵的力矩

處於外磁場的磁鐵會感受到外磁場施加的力矩，促使磁鐵的磁矩與外磁場呈相同方向。做簡單實驗就可以很容易地觀察到這現象：固定一塊條形磁鐵X於某位置，假若磁鐵X作用於條形磁鐵Y的磁場與磁鐵Y的磁矩呈不同方向，則會有力矩作用於磁鐵Y，促使磁鐵Y旋轉，使得磁鐵Y的磁矩與磁鐵X的磁場呈相同方向。磁矩為μ{displaystyle {boldsymbol {mu }}}的磁鐵Y，因為處於磁鐵X所產生的磁場B{displaystyle mathbf {B} }，而感受到的力矩τ{displaystyle {boldsymbol {tau }}}以方程式表示為

τ=μ×B{displaystyle {boldsymbol {tau }}={boldsymbol {mu }}times mathbf {B} }。

這現象可以解釋，為什麼在地球表面某位置的局域磁場方向，是指南針（或任意磁鐵）的指北極的指向。

磁場與磁矩耦合產生的力矩可以用來驅動簡單的電動機。在一個簡單的直流電動機設計圖裏，固定一塊磁鐵於自由旋轉的旋轉軸（稱為轉子），排列一組電磁鐵（稱為定子）於旋轉軸的外周。然後，開啟交流電通過每一塊電磁鐵，每一股電流與隔鄰的電流，其相位差是有限常定值。這樣，在旋轉軸位置，會造成旋轉磁場。感受到磁場施加的力矩，轉子的磁矩會趨於與磁場呈相同方向，因此，轉子會跟著旋轉磁場不停地旋轉。這就是電動機將電能轉換為機械能的基本運作機制。

假若逆反上述機制，則可將機械能轉換為電能。這是發電機的運作機制。

在後面旋轉磁場段落裏，還有更多有關這種使用電磁鐵的例子。

外磁場作用於磁鐵的磁力

高磁場區域會吸引或排斥磁鐵，決定於磁鐵與磁場之間的相對取向。這是個一般定則。異性磁極相互吸引，同性磁極相互排斥，就是這定則的特例。兩個磁鐵的異性磁極相互吸引，因為兩個異性磁極之間的磁場較強烈，而且這磁場與磁鐵的磁矩呈相同方向。

假設磁矩的方向被逆反，則結果也會被逆反。假設磁鐵的磁矩與磁場呈相反方向，而磁鐵又不會因為磁場施加的力矩而改變取向，則作用於磁鐵的磁力，其方向會朝向磁場比較微弱的區域，這對應於兩個磁鐵的同性磁極相互排斥。不均勻外磁場可以區分不同定向的磁偶極子，這是著名的施特恩－格拉赫實驗的運作原理。這實驗建立了原子及電子的磁偶極矩的量子性質^[13]。

處於不均勻外磁場B{displaystyle mathbf {B} }的磁鐵所感受到的磁力F{displaystyle mathbf {F} }，以方程式近似為

F=∇(μ⋅B){displaystyle mathbf {F} =mathbf {nabla } left({boldsymbol {mu }}cdot mathbf {B} right)}；

其中，μ{displaystyle {boldsymbol {mu }}}是磁鐵的磁矩。

注意到−μ⋅B{displaystyle -{boldsymbol {mu }}cdot mathbf {B} }是磁場與磁矩之間的作用能量。所以，作用力F{displaystyle mathbf {F} }的方向是朝向減少作用能量的方向。磁矩μ{displaystyle {boldsymbol {mu }}}固定不變，當磁場與磁矩呈相同方向時，作用力的方向是朝向磁場比較強的區域；當磁場與磁矩呈相反方向時，作用力的方向是朝向磁場比較弱的區域。這方程式對於零尺寸的磁鐵（磁偶極子）完全正確；對於其它小尺寸的磁鐵則是近似正確；對於大尺寸磁鐵，必須將其分為幾個小區域，再將每一個小區域的磁矩所感受到的磁力綜合為總磁力。

電流與磁場

電流會產生磁場。這電流可以是在導線內的巨觀電流，或是運動於原子軌域的電子所形成的微觀電流。處於外磁場的載流導線會感受到外磁場施加的磁力。

運動中的帶電粒子所生成的磁場

所有運動中的帶電粒子都會生成相當複雜、但眾所熟悉的磁場^{[notes 11]}。這磁場與粒子的帶電量、速度和加速度有關。

由於帶電粒子的運動不能形成電流，所以，必須應用推遲勢概念來計算其電場和磁場。假設一個帶有電量q{displaystyle q}的粒子以等速度v{displaystyle mathbf {v} }移動，在時間t{displaystyle t}的位置為w=vt{displaystyle mathbf {w} =mathbf {v} t}。那麼，馬克士威方程組給出此帶電粒子所生成在場位置為r{displaystyle mathbf {r} }的電場和磁場：

E=q4πϵ01−v2/c2(1−v2sin2⁡θ/c2)3/2r−w|r−w|3{displaystyle mathbf {E} ={frac {q}{4pi epsilon _{0}}}{frac {1-v^{2}/c^{2}}{(1-v^{2}sin ^{2}theta /c^{2})^{3/2}}}{frac {mathbf {r} -mathbf {w} }{|mathbf {r} -mathbf {w} |^{3}}}}、

B=v×1c2E{displaystyle mathbf {B} =mathbf {v} times {frac {1}{c^{2}}}mathbf {E} }；

其中，ϵ0{displaystyle epsilon _{0}}是電常數，c{displaystyle c}是光速，r{displaystyle mathbf {r} }是場位置，θ{displaystyle theta }是v{displaystyle mathbf {v} }和r−w{displaystyle mathbf {r} -mathbf {w} }之間的夾角。

這方程式最先由奧利弗·黑維塞於1888年推導出來。當v2≪c2{displaystyle v^{2}ll c^{2}}時，電場和磁場可以近似為

E=q4πϵ0 r−w|r−w|3{displaystyle mathbf {E} ={frac {q}{4pi epsilon _{0}}} {frac {mathbf {r} -mathbf {w} }{|mathbf {r} -mathbf {w} |^{3}}}}、

B=μ0qv4π×r−w|r−w|3{displaystyle mathbf {B} ={frac {mu _{0}qmathbf {v} }{4pi }}times {frac {mathbf {r} -mathbf {w} }{|mathbf {r} -mathbf {w} |^{3}}}}。

電場的方程式就是庫侖定律，磁場的方程式稱為「必歐-沙伐點電荷定律」^[14]。

電流產生的磁場

載流導線的電流I{displaystyle I}在周圍產生磁場B{displaystyle mathbf {B} }。磁場的方向可以用右手定則找出。

螺線管繪圖。

磁場線以同心圓圖樣環繞著載流導線。磁場的方向可以用右手定則找出，其大小與離載流導線的徑向距離呈平方反比。必歐-沙伐定律闡明，假設源位置為r′{displaystyle mathbf {r} '}的微小線元素dℓ ′{displaystyle mathrm {d} {boldsymbol {ell }}^{ prime }}載有電流I{displaystyle I}，則dℓ ′{displaystyle mathrm {d} {boldsymbol {ell }}^{ prime }}貢獻出的磁場dB{displaystyle mathrm {d} mathbf {B} }在場位置r{displaystyle mathbf {r} }為

dB=μ0I4πdℓ ′×r−r′|r−r′|3{displaystyle mathrm {d} mathbf {B} ={frac {mu _{0}I}{4pi }}mathrm {d} {boldsymbol {ell }}^{ prime }times {frac {mathbf {r} -mathbf {r} '}{|mathbf {r} -mathbf {r} '|^{3}}}}。

採用靜磁近似，當電流足夠緩慢地隨時間而改變時（例如當載流導線足夠緩慢地移動時），這定律成立。

將一根載流導線彎捲成為線圈。這動作會增強線圈內部的磁場，同時減弱線圈外部的磁場。將導線多重捲繞為緊密的多匝線圈，會增強這效應。這多匝線圈，稱為螺線管。在螺線管內加入鐵芯，會更加增強這效應，整個物體稱為電磁鐵，可以產生強大的，能被準確控制的磁場。長度超大於直徑的電磁鐵，可以近似其內部磁場為均勻磁場，近似其外部磁場為零。

在靜磁學裏，安培定律描述磁場與電流之間的關係。其積分形式與微分形式分別為

∮C⁡B⋅dℓ=μ0Ienc{displaystyle oint _{mathbb {C} }mathbf {B} cdot mathrm {d} {boldsymbol {ell }}=mu _{0}I_{mathrm {enc} }}、

∇×B=μ0J{displaystyle nabla times mathbf {B} =mu _{0}mathbf {J} }；

其中，C{displaystyle mathbb {C} }是路徑積分的閉迴路，Ienc{displaystyle I_{mathrm {enc} }}是閉迴路C{displaystyle mathbb {C} }所圍住的電流，J{displaystyle mathbf {J} }是電流密度。

對於穩定電流，安培定律恆成立。對於計算具有高度對稱性的案例，像無窮長導線或無窮長螺線管，安培定律特別有用。

假設電場含時間，則安培定律不正確，必需加以修正。將馬克士威修正項目加入安培定律的方程式，成為馬克士威-安培方程式：

∇×B=μ0J+μ0ϵ0∂D∂t{displaystyle nabla times mathbf {B} =mu _{0}mathbf {J} +mu _{0}epsilon _{0}{frac {partial mathbf {D} }{partial t}}}；

其中，D{displaystyle mathbf {D} }是電位移。

這是馬克士威方程組的四條方程式中之一條。

電流與磁力

移動中的帶電粒子所感受到的磁力

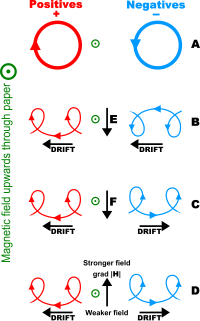
帶電粒子漂移（DRIFT）於均勻磁場中的軌跡。（A）沒有其它作用力干擾（B）添加電場E{displaystyle mathbf {E} }（C）添加恒力 F{displaystyle mathbf {F} }（例如：重力，（D）改為不均勻的磁場，∇|H|≠0{displaystyle nabla |H|neq 0}

移動於磁場中的帶電粒子會感受到勞侖茲力。其大小與磁場，粒子的帶電量、粒子垂直於磁場的移動速度成正比，以方程式表示，

F=qv×B{displaystyle mathbf {F} =qmathbf {v} times mathbf {B} }；

其中，F{displaystyle mathbf {F} }是勞侖茲力，q{displaystyle q}是粒子的帶電量，v{displaystyle mathbf {v} }是粒子的移動速度。

勞侖茲力必定垂直於B{displaystyle mathbf {B} }和v{displaystyle mathbf {v} }。固定不動的粒子或沿著磁場線移動的粒子都不會感受到任何勞侖茲力。帶電粒子繞著磁場線移動的軌跡是圓形的（更一般地，由於帶電粒子可能會沿著磁場線移動，軌跡是螺旋形的），這運動稱為迴旋運動（cyclotron motion）。由於磁力永遠垂直於移動方向，磁場不能做任何機械功於孤獨電荷。但是，磁場可以改變粒子的移動方向，甚至於使得感受到某外力作用的粒子會朝著垂直於那外力的方向漂移。時常，會有人士聲稱磁力可以做機械功於真實磁偶極子或束縛於某種作用力的帶電粒子。但是這些皆屬無稽之談^[15][16]。

載流導線所感受到的磁力

由於電流是一群移動中的帶電粒子所形成的巨觀效應，載流導線所感受到的磁力類似移動中的帶電粒子所感受到的磁力。處於磁場中的載流導線會感受到一種側向力。

假設電場為零，則作用於移動速度為v{displaystyle mathbf {v} }的電荷q{displaystyle q}的勞侖茲力是

F=qv×B{displaystyle mathbf {F} =qmathbf {v} times mathbf {B} }。

對於線電荷密度為λ{displaystyle lambda }的載流導線，總勞侖茲力為

F=∫Cv×B dq=∫Cv×Bλ dℓ=∫CI×B dℓ{displaystyle mathbf {F} =int _{mathbb {C} }mathbf {v} times mathbf {B} mathrm {d} q=int _{mathbb {C} }mathbf {v} times mathbf {B} lambda mathrm {d} ell =int _{mathbb {C} }mathbf {I} times mathbf {B} mathrm {d} ell }；

其中，C{displaystyle mathbb {C} }是積分路徑，I=λv{displaystyle mathbf {I} =lambda mathbf {v} }是電流向量。

假設電流是穩定電流，則可以將電流從積分內提出，用微小線元素向量dℓ{displaystyle mathrm {d} {boldsymbol {ell }}}來表示電流I{displaystyle mathbf {I} }的方向：

F=I∫Cdℓ×B{displaystyle mathbf {F} =Iint _{mathbb {C} }mathrm {d} {boldsymbol {ell }}times mathbf {B} }。

這公式給出了處於外磁場的載流導線所感受到的磁力。使用這公式和必歐-沙伐定律，就可以推導出安培力定律（詳盡細節，請參閱安培力定律）。

假設，磁場是均勻磁場，積分路徑是垂直於磁場的直線，則

F=ILB{displaystyle F=ILB}；

其中，L{displaystyle L}是積分路徑C{displaystyle mathbb {C} }的長度。

磁力的方向

右手開掌定則：使用右手，將大拇指朝著電流方向指去，再將其它四根手指朝著磁場方向指去，則掌心所面對的方向就是磁力的方向。

如左圖所示，電流、磁場與導線受力方向，三者之間的關係，可用「右手開掌定則」來決定：「將右手掌張開，四指指向磁場方向，大拇指張開，與四指垂直，指向導線的電流方向，則掌心推出的方向即為導線的受力方向，三者間兩兩相互垂直」。

由於正電荷移動的方向相反於負電荷移動的方向，但都會形成同樣方向的電流，只靠著測量產生的磁場，並不能分辨出到底是正電荷在移動還是負電荷在以相反方向移動。若要分辨出電荷載子的種類，必須施加外磁場，這外磁場垂直於電荷移動方向，使得電荷因感受到勞侖茲力而偏向一邊，從測量兩邊之間的電壓，可以偵測出到底是哪種電荷在移動。詳盡細節，請參閱條目霍爾效應。

磁性物質內外的H場與B場

當計算磁場時，假若用總電流為參數，則前面推導出來的磁場方程式正確無誤。但是，處於外磁場的磁性物質會生成自己的束縛電流，計算這束縛電流可能頗費工夫。這束縛電流是由原子尺寸載流迴圈，與物質內部像電子一類的亞原子粒子的自旋，共同形成的。假若改計算先前定義的H場，則可避免計算束縛電流，但在學習這技巧之前，必須先了解磁化強度概念。

磁化強度

磁化強度M{displaystyle mathbf {M} }描述物質的磁化程度，定義為單位體積的磁偶極矩，以方程式表示為

M =def nμ{displaystyle mathbf {M} {stackrel {def}{=}} n{boldsymbol {mu }}}；

其中，n{displaystyle n}是磁偶極子密度，μ{displaystyle {boldsymbol {mu }}}是磁偶極子的磁偶極矩。

當施加外磁場於磁性物質時，磁性物質的內部會被磁化，會出現眾多磁偶極子。磁化強度計量磁性物質被磁化的程度。採用國際單位制，磁化強度的單位是安培／公尺，方向是巨觀的平均磁偶極矩的方向。一個均勻磁鐵的磁化強度乘以體積，就可以得到這磁鐵的磁矩。與B場不同，磁化強度只存在於磁性物質內部。因此，磁化強度場線開始與終結於磁極。

合乎物理理論的正確計算方法是，總和所有產生磁化強度的磁偶極子的電流，得到的電流稱為束縛電流，這是磁性物質用來產生磁場的源頭。按照這方法，磁性物質內部的束縛電流密度Jb{displaystyle J_{b}}和表面束縛電流密度Kb{displaystyle K_{b}}分別為

Jb =def ∇×M{displaystyle J_{b} {stackrel {def}{=}} nabla times mathbf {M} }、

Kb =def M×n^{displaystyle K_{b} {stackrel {def}{=}} mathbf {M} times {hat {n}}}；

其中，n^{displaystyle {hat {n}}}是垂直於磁性物質表面的單位向量。

從這些束縛電流密度，可以計算出磁化強度所貢獻的磁場。

H場與磁性物質

H場H{displaystyle mathbf {H} }定義為

H =def Bμ0−M{displaystyle mathbf {H} {stackrel {def}{=}} {frac {mathbf {B} }{mu _{0}}}-mathbf {M} }。

使用H場H{displaystyle mathbf {H} }的優點是它與束縛源無關，只涉及自由源。例如，將H{displaystyle mathbf {H} } 路徑積分於閉迴路C{displaystyle mathbb {C} }，會得到穿過閉迴路C{displaystyle mathbb {C} }內部的淨自由電流If{displaystyle I_{mathrm {f} }}（不包括束縛電流Ib{displaystyle I_{mathrm {b} }} )：

∮C⁡H⋅dℓ=∮C⁡(Bμ0−M)⋅dℓ=Itot−Ib=If{displaystyle oint _{mathbb {C} }mathbf {H} cdot mathrm {d} {boldsymbol {ell }}=oint _{mathbb {C} }left({frac {mathbf {B} }{mu _{0}}}-mathbf {M} right)cdot mathrm {d} {boldsymbol {ell }}=I_{mathrm {tot} }-I_{mathrm {b} }=I_{mathrm {f} }}。

應用磁荷的概念，將H{displaystyle mathbf {H} }曲面積分於任意閉曲面S{displaystyle mathbb {S} }，會捕獲所有在閉曲面S{displaystyle mathbb {S} }內的磁荷qM{displaystyle q_{M}}：

∮S⁡H⋅da=∮S⁡(Bμ0−M)⋅da=(0+qM)=qM{displaystyle oint _{mathbb {S} }mathbf {H} cdot mathrm {d} mathbf {a} =oint _{mathbb {S} }left({frac {mathbf {B} }{mu _{0}}}-mathbf {M} right)cdot mathrm {d} mathbf {a} =(0+q_{M})=q_{M}}。

磁性物質

由於外磁場的作用，磁性物質會響應出磁化強度和由這磁化強度產生的磁場。這響應通常很微弱，只有在外磁場作用時才會存在。「磁性」這術語專門形容這些物質如何響應，並且用來分類物質的磁相。按照各種物質的磁性行為，可以分為幾類：

• 
  抗磁性物質響應出的磁化強度與外磁場呈相反方向，會趨於朝著磁場較弱的區域移動，即被磁場排斥^[17]。


• 
  順磁性物質響應出的磁化強度與外磁場呈相同方向，會趨於朝著磁場較強的區域移動，即被磁場吸引^[17]。


• 
  鐵磁性物質內部有很多未配對電子。由於交換作用（exchange interaction），這些電子的自旋趨於與相鄰未配對電子的自旋呈相同方向。由於鐵磁性物質內部又分為很多磁疇，雖然磁疇內部所有電子的自旋會單向排列，造成「飽和磁矩」，磁疇與磁疇之間，磁矩的方向與大小都不相同。所以，未被磁化的鐵磁性物質，其淨磁矩與磁化向量都等於零。假設施加外磁場，這些磁疇的磁矩還趨於與外磁場呈相同方向，從而形成有可能相當強烈的磁化向量與其感應磁場。隨著外磁場的增高，磁化強度也會增高，直到「飽和點」，淨磁矩等於飽合磁矩。這時，再增高外磁場也不會改變磁化強度。假設現在撤除外磁場，則鐵磁性物質仍能保存一些磁化的狀態，淨磁矩與磁化向量不等於零。所以，經過磁化處理後的鐵磁性物質具有「自發磁矩」。


• 
  反鐵磁性物質內部的相鄰價電子的自旋趨於相反方向。這種物質的淨磁矩與磁化強度都等於零。大多數反鐵磁性物質只存在於低溫狀況。假設溫度超過奈爾溫度，則通常會變為順磁性物質。


• 
  亞鐵磁性物質內部是由兩種以上原子組成，不同次晶格的不同原子，其磁矩的方向相反，數值大小不相等，所以，淨磁矩與磁化強度都不等於零，具有較微弱的鐵磁性。


• 
  超導體（和鐵磁超導體）^[18][19]：當溫度低於某臨界溫度，磁場小於某臨界磁場時，這些物質會特徵地變成完美導電體，電導率變得無窮大，磁性也變得非常顯著，當磁場小於某更小的臨界磁場時，這物質會成為完美抗磁性物質。超導體常常會在某寬廣的溫度和磁場值域內（稱為「混合態」），展現出磁化強度對於磁場的複雜磁滯依賴關係。

對於順磁性物質或抗磁性物質，磁化強度M{displaystyle mathbf {M} }與H場H{displaystyle mathbf {H} }之間的關係通常是線性關係：

M=χmH{displaystyle mathbf {M} =chi _{m}mathbf {H} }；

其中，χm{displaystyle chi _{m}}是磁化率。

因此，B場B{displaystyle mathbf {B} }與H場H{displaystyle mathbf {H} }之間的關係為

B=μ′H{displaystyle mathbf {B} =mu 'mathbf {H} }；

其中，μ′=μ0(1+χm){displaystyle mu '=mu _{0}(1+chi _{m})}是磁導率。

對於某些物質，磁導率可能是一個二階張量，B場與H場可能呈不同方向。這些B場與H場之間的關係是本構方程式（constitutive equation）的例子。超導體和鐵磁性物質的B場與H場之間的關係更加複雜。詳盡細節，請參閱磁滯現象。

電磁學：電場與磁場之間的關係

法拉第電磁感應定律：含時磁場生成的電場

在時間t{displaystyle t}，以閉迴路C{displaystyle mathbb {C} }為邊緣的曲面S{displaystyle mathbb {S} }，和在此曲面S{displaystyle mathbb {S} }某些位置的磁場B(r,t){displaystyle mathbf {B} (mathbf {r} ,,t)}。

在時間t{displaystyle t}通過任意曲面S{displaystyle mathbb {S} }的磁通量ΦB(t){displaystyle Phi _{B}(t)}定義為

ΦB(t) =def ∫SB(r,t)⋅da{displaystyle Phi _{B}(t) {stackrel {def}{=}} int _{mathbb {S} }mathbf {B} (mathbf {r} ,,t)cdot mathrm {d} mathbf {a} }；

其中，ΦB{displaystyle Phi _{B}}是磁通量，r{displaystyle mathbf {r} }是場位置，da{displaystyle mathrm {d} mathbf {a} }是微小面元素。

法拉第電磁感應定律闡明，通過任意曲面的磁通量變化率的負值，等於這任意曲面的邊緣所形成的封閉迴路的電動勢：

E=−dΦBdt{displaystyle {mathcal {E}}=-{frac {mathrm {d} Phi _{B}}{mathrm {d} t}}}。

假設曲面S{displaystyle mathbb {S} }固定不動，則磁通量對於時間的全導數可以改為偏導數，可以移進積分符號：

E=−∂ΦB∂t=−∫S∂B∂t⋅da{displaystyle {mathcal {E}}=-{frac {partial Phi _{B}}{partial t}}=-int _{mathbb {S} }{frac {partial mathbf {B} }{partial t}}cdot mathrm {d} mathbf {a} }。

根據法拉第電磁感應定律，含時磁場會生成電動勢。假設，一塊磁鐵移動通過導環圈，由於磁場是含時磁場，會生成電動勢，驅使感應電流於導環圈。這是許多電動機和發電機的運作原理，注意到法拉第電磁感應方程式內的負號是必需的，它意味著感應電流所生成磁場會反抗這含時磁場的改變。這現象稱為冷次定律。

與靜電學裏電場的物理行為迥然不同，電場沿著閉迴路的電場環流量不等於零，而會等於電動勢^[20]：

E=∮C⁡E⋅dℓ{displaystyle {mathcal {E}}=oint _{mathbb {C} }mathbf {E} cdot mathrm {d} {boldsymbol {ell }}}；

其中，E{displaystyle mathbf {E} }是電場，C{displaystyle mathbb {C} }是曲面S{displaystyle mathbb {S} }邊緣的閉迴路。

所以，沿著閉迴路C{displaystyle mathbb {C} }的電場與通過曲面S{displaystyle mathbb {S} }的磁場之間的關係為

∮C⁡E⋅dℓ=−∫S∂B∂t⋅da{displaystyle oint _{mathbb {C} }mathbf {E} cdot mathrm {d} {boldsymbol {ell }}=-int _{mathbb {S} }{frac {partial mathbf {B} }{partial t}}cdot mathrm {d} mathbf {a} }；

應用斯托克斯定理，這積分方程式可以變為微分方程式：

∇×E=−∂B∂t{displaystyle nabla times mathbf {E} =-{frac {partial mathbf {B} }{partial t}}}；

這是馬克士威方程組的四條方程式中的一條。

馬克士威-安培方程式：含時電場生成的磁場

1861年，馬克士威將安培定律方程式重新推導一遍，使得符合電動力學條件，並且發表結果於論文《論物理力線》內。馬克士威認為，含時電場會生成磁場，假若電場含時間，則前述安培定律方程式不成立，必須加以修正。經過修正後，新的方程式稱為馬克士威-安培方程式，是馬克士威方程組中的一個方程式，以積分形式表示為

∮C⁡B⋅dℓ=μ0∫S(J+∂D∂t)⋅da{displaystyle oint _{mathbb {C} }mathbf {B} cdot mathrm {d} {boldsymbol {ell }}=mu _{0}int _{mathbb {S} }left(mathbf {J} +{frac {partial mathbf {D} }{partial t}}right)cdot mathrm {d} mathbf {a} }；

其中，S{displaystyle mathbb {S} }是邊緣為C{displaystyle mathbb {C} }的任意曲面，J{displaystyle mathbf {J} }是曲面S{displaystyle mathbb {S} }的電流密度，D{displaystyle mathbf {D} }是電位移。

以微分形式表示，

∇×B=μ0J+μ0ϵ0∂E∂t{displaystyle nabla times mathbf {B} =mu _{0}mathbf {J} +mu _{0}epsilon _{0}{frac {partial mathbf {E} }{partial t}}}。

位移電流密度JD{displaystyle mathbf {J} _{D}}定義為

JD =def ∂D∂t{displaystyle mathbf {J} _{D} {stackrel {def}{=}} {frac {partial mathbf {D} }{partial t}}}。

位移電流密度分為兩個部分：

JD=ε0∂E∂t+∂P∂t{displaystyle mathbf {J} _{D}=varepsilon _{0}{frac {partial mathbf {E} }{partial t}}+{frac {partial mathbf {P} }{partial t}}}；

其中，P{displaystyle mathbf {P} }是電極化強度。

這方程式右手邊的第一個項目是馬克士威修正項目，在任何地方都可存在，甚至在真空也可存在，雖然不涉及任何真實的電荷運動，但是，它描述一個含時電場的物理行為，就好像是真實的電流。第二個項目是電極化電流密度，與電介質內單獨分子的極化性有關。由於增添了位移電流，電場與磁場能夠以電磁波的形式傳播於空間（詳盡細節，請參閱電磁波條目）。

馬克士威方程組

從馬克士威方程組，馬克士威於1865年推導出電磁波方程式，一種波動方程式，這清楚地顯示出電場和磁場的波動本質。因為電磁波方程式預測的電磁波速度與光速的測量值相等，馬克士威推論光波也是電磁波。

與所有向量場一樣，磁場具有兩種重要的數學性質，將磁場與其源頭（對於磁場而言，即電流和含時電場）連結。這兩個性質與電場的兩個對應性質，在馬克士威方程組裏，表達的淋漓盡致。馬克士威方程組和勞侖茲力方程式可以完整地解釋經典電磁學裡所有的現象和效應。

第一種數學性質是向量場的散度∇⋅Z{displaystyle nabla cdot mathbf {Z} }，即向量場Z{displaystyle mathbf {Z} }怎樣從某一點流出。如同前面所述，磁場線永遠不會開始或終結於某一點，其磁場線會形成一完整迴路。用數學說法，就是磁場的散度等於零（這種向量場稱為零散度向量場，或螺線向量場）。高斯磁定律專門陳述這性質，也就是磁荷不存在，或磁單極子不存在的事實。迥然不同，電場線開始或終結於電荷，其散度不等於零，與電荷密度成正比。這性質稱為高斯定律。

第二種數學性質是向量場的旋度∇×Z{displaystyle nabla times mathbf {Z} }，即向量場Z{displaystyle mathbf {Z} }怎樣彎捲或環繞於某一點。旋度的結果是環流源頭的狀況。磁場和電場的旋度方程式分別為馬克士威-安培方程式和法拉第電磁感應方程式。

簡短地說，馬克士威方程組的四個方程式分別為：電荷是如何產生電場的高斯定理；論述了磁單極子的不存在的高斯磁定律；電流和含時電場是怎樣產生磁場的馬克士威-安培定律，以及含時磁場是怎樣產生電場的法拉第電磁感應定律。採用國際單位制，馬克士威方程組表示為

以總電荷和總電流為源頭的表述

名稱	微分形式	積分形式
高斯定律	∇⋅E=ρε0{displaystyle nabla cdot mathbf {E} ={frac {rho }{varepsilon _{0}}}}	∫SE⋅da=Qε0{displaystyle int _{mathbb {S} }mathbf {E} cdot mathrm {d} mathbf {a} ={frac {Q}{varepsilon _{0}}}}
高斯磁定律	∇⋅B=0{displaystyle nabla cdot mathbf {B} =0}	∫SB⋅da=0{displaystyle int _{mathbb {S} }mathbf {B} cdot mathrm {d} mathbf {a} =0}
法拉第電磁感應定律	∇×E=− ∂B∂t{displaystyle nabla times mathbf {E} =- {frac {partial mathbf {B} }{partial t}}}	∮C⁡ E⋅dℓ=− dΦBdt{displaystyle oint _{mathbb {C} } mathbf {E} cdot mathrm {d} {boldsymbol {ell }}=- {frac {mathrm {d} Phi _{mathbf {B} }}{mathrm {d} t}}}
馬克士威-安培定律	∇×B=μ0J+μ0ε0∂E∂t {displaystyle nabla times mathbf {B} =mu _{0}mathbf {J} +mu _{0}varepsilon _{0}{frac {partial mathbf {E} }{partial t}} }	∮C⁡ B⋅dℓ=μ0I+μ0ε0dΦEdt{displaystyle oint _{mathbb {C} } mathbf {B} cdot mathrm {d} {boldsymbol {ell }}=mu _{0}I+mu _{0}varepsilon _{0}{frac {mathrm {d} Phi _{mathbf {E} }}{mathrm {d} t}}}

其中，ρ{displaystyle rho }是電荷密度，Q{displaystyle Q}是總電荷量，ΦE{displaystyle Phi _{E}}是電通量。

如同前面所述，響應外電場或外磁場，物質會自己製造出對應的束縛電荷或束縛電流，這些物理量的計算比較麻煩。為了避開這問題，可以使用H場和電位移場，這樣，馬克士威方程組可以以自由電流密度Jf{displaystyle mathbf {J} _{f}}和自由電荷密度ρf{displaystyle rho _{f}}來重新表述：

以自由電荷和自由電流為源頭的表述

名稱	微分形式	積分形式
高斯定律	∇⋅D=ρf{displaystyle nabla cdot mathbf {D} =rho _{f}}	∫SD⋅da=Qf{displaystyle int _{mathbb {S} }mathbf {D} cdot mathrm {d} mathbf {a} =Q_{f}}
高斯磁定律	∇⋅B=0{displaystyle nabla cdot mathbf {B} =0}	∫SB⋅da=0{displaystyle int _{mathbb {S} }mathbf {B} cdot mathrm {d} mathbf {a} =0}
法拉第電磁感應定律	∇×E=− ∂B∂t{displaystyle nabla times mathbf {E} =- {frac {partial mathbf {B} }{partial t}}}	∮C⁡ E⋅dℓ=− dΦBdt{displaystyle oint _{mathbb {C} } mathbf {E} cdot mathrm {d} {boldsymbol {ell }}=- {frac {mathrm {d} Phi _{mathbf {B} }}{mathrm {d} t}}}
馬克士威-安培定律	∇×H=Jf+∂D∂t{displaystyle nabla times mathbf {H} =mathbf {J} _{f}+{frac {partial mathbf {D} }{partial t}}}	∮C⁡ H⋅dℓ=If+dΦDdt{displaystyle oint _{mathbb {C} } mathbf {H} cdot mathrm {d} {boldsymbol {ell }}=I_{f}+{frac {mathrm {d} Phi _{mathbf {D} }}{mathrm {d} t}}}

這方程組並不比原本方程組更具有一般性。解析整個問題，還需要補足B場與H場之間的關係式，和電場與電位移場之間的關係式。但是，當這些關係式很簡單時，則可以避免計算束縛電荷和束縛電流。

電場與磁場：同樣現象的不同表態

根據狹義相對論，電磁力的分隔為電場部分和磁場部分並不具有絕對性，而是依觀測者的參考系而定；在某一參考系的觀測者所觀測到的純電場力，在另一參考系的觀測者可能會觀測為電場力與磁場力的合力；又在某一參考系的觀測者所觀測到的純磁場力，在另一參考系的觀測者可能會觀測為電場力與磁場力的合力。

更具體地說，在狹義相對論裏，電場與磁場綜合成為二階張量，稱為電磁張量。改變參考系會攪混這電磁張量的分量，改變每一個分量的數值。這種綜合類似於狹義相對論將時間與空間綜合成為時空，或將動量與能量綜合成為四維動量。

磁向量勢

像所有的軸向量一樣，經過鏡子反射，磁場會改變正負號。一條載流迴圈（黑色），經過鏡子（虛線）反射，則載流迴圈所產生的磁場，不只是被鏡子反射，而是被反射與逆反。

在進階學術領域裏，像量子力學或相對論，使用位勢來表述電動力學，而不使用電場或磁場，是一種比較便利的方法。採用位勢表述，磁向量勢A{displaystyle mathbf {A} }與電勢φ{displaystyle varphi }分別如此定義：

B=∇×A{displaystyle mathbf {B} =nabla times mathbf {A} }、

E=−∇φ−∂A∂t{displaystyle mathbf {E} =-nabla varphi -{frac {partial mathbf {A} }{partial t}}}。

磁向量勢A{displaystyle mathbf {A} }可以詮釋為「廣義勢動量每單位電荷」^[21]，就如同電勢φ{displaystyle varphi }詮釋為廣義勢能每單位電荷。

從數學方面來說，由於磁場是一個向量叉積運作的結果，磁場是一種軸向量（axial vector）。如右圖所示，由於右手定則嚴格要求，在鏡子裏看到的一條載流迴圈，其生成的磁場在鏡子裏的鏡像會被逆反，而普通向量，像速度向量，只會顯示出其鏡像。

馬克士威方程組，假若以位勢表達，可以鑄造成一種令人滿意的形式，特別適用於狹義相對論^[22]。A{displaystyle mathbf {A} }與φ{displaystyle varphi }共同綜合成電磁四維勢。使用電磁四維勢比較使用電磁張量簡單的多，又可以很容易地修改成合乎量子力學的形式。

量子電動力學

在現代物理學裏，物理學家認為電磁場不是經典場，而是量子場；電磁場不是由在空間的每一點具有三個數值的向量所代表，而是在每一個點具有三個量子算符的向量。量子電動力學是一種能夠準確地描述電磁作用的理論^[23]。量子電動力學被包括於一種更完備的理論，稱為粒子物理學的標準模型。

在量子電動力學裏，帶電粒子（或反粒子）彼此之間的電磁作用，是使用微擾理論計算獲得；這相當複雜的公式可以用費曼圖表現出來；在費曼圖裏，帶電粒子藉著互相交換虛光子來完成彼此之間的電磁作用。

量子電動力學應是物理史上最為準確的物理理論。量子電動力學的理論預測與實驗結果的相符合能夠達到非常高的準確度：現在大約為10⁻¹²（限制於實驗誤差）^[24]。更詳盡細節，請參閱條目高準確度量子電動力學實驗（precision tests of QED）

這篇文章內所有展示的方程式都是取經典近似而得到的，無法用來解釋量子現象與效應，但是，對於大多數日常狀況，應是綽綽有餘。

重要應用領域

地磁場

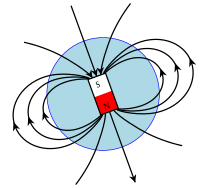
地磁場示意圖將地球的磁場源表示為一塊大磁鐵，其指南極是在地球的地磁北極下面很深的位置。

地核的外核部分含有熔化的鐵金屬和鎳金屬。科學家認為，這熔液的對流運動會產生從東方朝向西方的電流，繼而產生磁場，即「地磁場」。這理論稱為發電機理論。由於地磁場的存在，放置於地球表面任意位置的指南針，其指北極會指向北方，指向地球的地磁北極。這性質通常可以用來定義磁鐵的指北極。假設地球被視為一塊大磁鐵，因為異性磁極相互吸引，同性磁極相互排斥，這塊大磁鐵的指南極應該在地磁北極附近，其指北極應該在地磁南極附近。

右圖顯示出地磁場的磁場線。在地球表面大多數位置，除了南／北分量以外，磁場還具有顯著的上／下分量。由於地球的磁極與地極並不恰巧重複在一起，磁場具有些微的東／西分量。

地磁場不是毫無變化的，它的強度與地磁極位置會改變。科學家發現，地磁極會週期性地逆反定向，這過程稱為地磁反轉。最近一次的反轉是大約78萬年前的布容尼斯－松山反轉。對於澳大利亞紅英安岩和枕狀玄武岩的古地磁學研究發現，地磁場的存在，估計至少35億年之久^[25]。地磁場會在太空與太陽風和其它帶電粒子群流互相作用，因而形成磁層。地球磁層並不是球狀的，在面對太陽的一面，其邊界離地心的距離約為七萬千米（隨太陽風強度的不同而變化）。

旋轉磁場

由三捲不同相位線圈產生的磁場（以藍色箭矢表示）所形成的旋轉磁場。

理想的旋轉磁場會以等角速度改變磁場方向。旋轉磁場是交流電動機運作的重要機制。尼古拉·特斯拉在他的自傳裡寫到，於1882年，他想出了旋轉磁場的點子。1888年，他在這方面的研究成果獲得美國專利 381,968。

使用兩捲線圈，彼此的磁場方向互相垂直，各自通過的交流電的相位差為90°，就可以製出旋轉磁場。使用三捲彼此之間的幾何角度為120°的線圈，各自通過的電流，大小相同，相位差為120°，可以製出旋轉磁場。三相系統能夠製出適用於電動機的高品質旋轉磁場，這是全世界大多數電力供應系統都使用三相系統的主要原因之一。

霍爾效應

霍爾效應實驗證實，金屬導體的電荷載子是電子，而不是離子。

如左圖所示，假設，處於磁場的一條寬片型載流導線，其電流垂直於磁場，則其電荷載子會因為感受到勞侖茲力而偏向一邊，從而在垂直於磁場、電流的方向產生電壓於導線兩側。1879年，艾德溫·霍爾（Edwin Hall）發現這效應，稱為霍爾效應。由於能夠辨明電荷載子到底帶有正電還是帶有負電，這效應最先證實，在載流導線裏流動的電流，是由移動中的電子形成的，與質子無關。

磁強計應用霍爾效應為運作原理，可以用來測量磁場，或檢查像不銹鋼管道一類物體因腐蝕而產生的磁通量泄漏（magnetic flux leakage）。由於霍爾效應元件產生的訊號幅值非常微弱，必須加以放大，才能被偵測，所以，現在許多霍爾效應感測器都加入一個高增益積體電路放大器。霍爾效應感測器可以用來測量磁場、旋轉速度、液體流速、電流、壓力等等。

在半導體領域，霍爾效應也可以應用於偵測在半導體一類物質內的主要電荷載子是負電子還是正電洞。

霍爾效應推進器是一種低功率的離子推進器。當太空船進入軌道或太空時，可以用霍爾效應推進器來推進太空船。

磁路

H場在磁路學領域很有用處。在一個線性物質內部，

B=μ′H{displaystyle mathbf {B} =mu 'mathbf {H} }；

其中，μ′{displaystyle mu '}是磁導率。

這方程式的形式與歐姆定律很類似：

J=σE{displaystyle mathbf {J} =sigma mathbf {E} }；

其中，J{displaystyle mathbf {J} }是電流密度，σ{displaystyle sigma }是電導，E{displaystyle mathbf {E} }是電場。

將這比擬加以延伸，在靜磁學裏相當於巨觀歐姆定律I=V/R{displaystyle I=V/R}的是

Φ=FRm{displaystyle Phi ={frac {F}{R}}_{m}}；

其中，Φ=∫B⋅da{displaystyle Phi =int mathbf {B} cdot mathrm {d} mathbf {a} }是電路的磁通量，F=∫H⋅dl{displaystyle F=int mathbf {H} cdot mathrm {d} mathbf {l} }是磁動勢，Rm{displaystyle R_{m}}是磁阻。

採用這比擬，借用電路理論（circuit theory）發展出的技巧，可以很直接地計算複雜磁場幾何的磁通量。

磁场生物效应

磁场生物效应指的是外加磁场对生物的作用和影响，可能是有益的，也可能是有害的。磁场对生物的影响与磁场强度、磁场均匀度以及磁场是否随时间变化等因素有关。如果一个人在强度超过2T磁场中运动，就会感到眩晕和恶心，有时候口中有金属的味道并有视闪烁感。当磁场强度超过8T时，可能造成心室纤维颤动，而有生命危险。国际非电离辐射保护委员会建议在工作日中职业暴露的时量平均值应不超过200mT，最高限值为2T。对于一般公众的连续暴露限值为40mT。如果体内有起搏器等金属器件，则应回避超过0.5mT的静电磁场。^[26]

參閱

• 磁流體力學


• 發電機原理


• 磁場觀察膜


• 亥姆霍茲線圈

註釋

1. 
   ^ 更精確地分類，磁場是一種贗矢量。力矩和角速度也是準向量。當坐標被反演時，準向量會保持不變。
   


2. 
   ^ 基本粒子，像電子或正子等等，會產生自己內有的磁場，這是一種相對論性效應，並不是因為粒子運動而產生的。但是，對於大多數狀況，這磁場可以模想為是由粒子所載有的電荷因為旋轉運動而產生的。因此，這相對論性效應稱為自旋。磁鐵產生的磁場主要是由內部未配對電子的自旋形成的。
   


3. 
   ^ 他的論文《Epistola Petri Peregrini de Maricourt ad Sygerum de Foucaucourt Militem de Magnete》，簡稱為《Epistola de magnete（磁石書信）》，發表日期認定為公元1269年。
   


4. 
   ^ 按照磁化強度的定義，在這模型裡，類比彈簧的物理，為了要將磁化強度增加δM{displaystyle delta mathbf {M} }，拉扯與扭轉磁荷之間的相互作用，所需的機械功每單位體積為δW=H⋅μ0δM{displaystyle delta W=mathbf {H} cdot mu _{0}delta mathbf {M} }。由於磁場為B=μ0(H+M){displaystyle mathbf {B} =mu _{0}(mathbf {H} +mathbf {M} )}，包括了製備外磁場於真空所需的H場項目。所以，增加磁場所需的機械功每單位體積為δW=H⋅μ0δB{displaystyle delta W=mathbf {H} cdot mu _{0}delta mathbf {B} }。這是正確的結果。但是，用來推導的模型並不正確。
   


5. 
   ^ ，回顧沉思，這模型的成功，大多是因為，在磁性物質外部，電偶極子的電場跟磁偶極子的磁場有相同的樣式。只有在磁性物質內部，簡單的磁荷模型無法解釋磁場的物理行為。
   


6. 
   ^ Edward Purcell, in Electricity and Magnetism, McGraw-Hill, 1963, writes, Even some modern writers who treat B as the primary field feel obliged to call it the magnetic induction because the name magnetic field was historically preempted by H. This seems clumsy and pedantic. If you go into the laboratory and ask a physicist what causes the pion trajectories in his bubble chamber to curve, he'll probably answer "magnetic field", not "magnetic induction." You will seldom hear a geophysicist refer to the Earth's magnetic induction, or an astrophysicist talk about the magnetic induction of the galaxy. We propose to keep on calling B the magnetic field. As for H, although other names have been invented for it, we shall call it "the field H" or even "the magnetic field H."
   David Griffith, in Introduction to Electrodynamics, Prentice-Hall, Inc, 1999, page 271, writes, Many author call H, not B, the "magnetic field." Then, they have to invent a new word for B? the "flux density," or magnetic "induction"(an absurd choice, since that term already has at least two other meanings in electrodynamics). Anyway, B is indisputably the fundamental quantity, so I shall continue to call it the "magnetic field," as everyone does in the spoken language. H has no sensibile name: just call it "H".
   Andrew Zangwill, in Modern Electrodynamics, Cambridge University Press, 2013, page 44, writes, In this book, only the "electric field" E and the "magnetic field" B are fundamental. We give no special names to the auxiliary fields D and H.
   


7. 
   ^ 。試想將一個指南針置入磁鐵內部，指南針的指北極會指向磁鐵的指北極。又將兩塊條形磁鐵，端點連著端點，排列於一直線，假設相連結的兩個端點是磁異性，則兩塊條形磁鐵會相吸引，否則，兩塊條形磁鐵會相排斥。
   


8. 
   ^ 如同前面所述，磁場線的密度與磁場大小有關。
   


9. 
   ^ 曾經有幾個實驗製備出最初被認為可能是磁單極子的事件，但後來都無法獲得學術界確認。詳盡細節，請參閱磁單極子。
   


10. 
    ^ 這裡，微小的意思是，觀測者離磁鐵足夠的遙遠，這樣，磁鐵的尺寸可以被設定為無窮小；當尺寸驅向無窮小極限時，磁鐵可以理想化成為磁偶極子。較大尺寸的磁鐵的磁場必須包括更多項目，不只是與磁矩有關，還會與磁鐵的幾何形狀有關。
    


11. 
    ^ 根據狹義相對論，移動中的帶電粒子會產生電場和磁場，而對於處於與粒子同速度的參考系的觀察者，粒子是固定不動的，所以，只可能會產生電場。同樣的物理原則應該可以應用於各個不同的參考系，這意味著電場和磁場是同樣物理現象的兩面。更詳盡細節，請參閱條目經典電磁學與狹義相對論（classical electromagnetism and special relativity）。
    

參考文獻

進階閱讀

• 
  Griffiths, David J., Introduction to Electrodynamics(3rd ed.), Prentice Hall, 1998, ISBN 0-13-805326-X 
  


• 
  Jackson, John D., Classical Electrodynamics(3rd ed.), John Wiley & Sons, 1999, ISBN 0-471-30932-X, OCLC 224523909 
  


• 
  Tiple, Paul, Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics(5th ed.), W. H. Freeman, 2004, ISBN 0-7167-0810-8, OCLC 51095685 
  

查 论 编 电磁学 靜電學 電荷 電場 導體 絕緣體 摩擦起電效應 静电放电 静电感应 库仑定律 高斯定律 电通量 电势能 电偶极矩 電極化 電位移 靜磁學 安培定律 磁場 磁化强度 磁通量 毕奥-萨伐尔定律 磁矩 高斯磁定律 磁矢勢 电动力学 洛伦兹力 電磁感應 法拉第电磁感应定律 楞次定律 位移電流 馬克士威方程組 电磁场 电磁波 馬克士威應力張量 坡印廷向量 黎納-維謝勢 傑斐緬柯方程式 渦電流 倫敦方程 推遲勢 自由空間 电路 电流 電勢 電壓 电阻 欧姆定律 串聯電路 並聯電路 直流電 交流電 带电流 中性流 電動勢 電容 电感 阻抗 电导 波导 憶阻器 基爾霍夫電路定律 協變表述 電磁張量 四維電流密度 電磁應力-能量張量 四維勢 发展史 庫侖 安培 高斯 奧斯特 亨利 法拉第 馬克士威 黑維塞 韋伯 特斯拉 勞侖茲 赫茲 伏打