Vrstjr

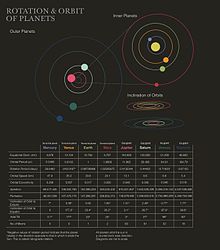
行星的轨道

兩個在質量上差異不大的物體會繞著共同質心運轉。圖中這個獨特的軌道，是相似於冥王星和查龍的系統。

在物理学中，轨道是一个物体在引力作用下绕空间中一点运行的路径，比如行星绕一颗恒星的轨迹，或天然卫星绕一颗行星的轨迹。行星的轨道一般都是椭圆，而且其绕行的质量中心在椭圆的一个焦点上。

当前人们对轨道运动原理的认识基于爱因斯坦的广义相对论，认为引力是由时空弯曲造成的，而轨道则是时空场的几何测地线。为了简化计算，通常用基于开普勒定律的万有引力理论来作为相对论的近似。

历史

历史上，人们用本轮来描述行星的视运动，认为行星的运动是很多圆周运动合成的结果，这是一种几何方法，并没有涉及引力的概念。在开普勒证明行星的运动轨迹是椭圆之前，用这种方法来预测行星的轨迹勉强可行。

最开始，人们使用以地球为中心的太阳系天球模型来解释行星的视运动。该模型假设存在一个完美的球体或圆环，所有的恒星和行星都在其表面运动。在更精确的测量了行星的运动后，人们引入了均轮和本轮这样的理论来描述行星运动。这种系统能更精确的预测行星的位置，但随着测量结果越来越精确，需要加入更多的本轮到模型中，因此，这种模型变得越来越繁琐。

17世紀初，在约翰内斯·开普勒對大量精密觀察的天體軌道數據進行分析後，得出著名的3个行星运动定律。第一，他发现太阳系中行星轨道不是以往人们想象的正圆形，而是椭圆的；太阳也不是位于轨道中心，而是在一个焦点上。第二，行星的轨道速度，也不是恒定不變的，事實上行星的軌道速度與當下行星至太阳的距离有關。第三，他歸納出可通用於太阳系所有行星轨道性質的數學关系：行星到太阳距离的立方（以天文单位（AU）计算）等于行星轨道周期的平方（以地球年计算）。以木星為例，它到太阳的距离約為5.2AU，轨道周期約为11.86地球年，則滿足數學關係：5.23≈11.862{displaystyle 5.2^{3}approx 11.86^{2}}。

到了1687年，艾萨克·牛顿在他的万有引力理论中证明了开普勒定律。一般而言，物體在單純重力作用下的運動軌道都屬於圓錐曲線。牛頓表示，兩個天體在互相環繞的軌道上時，个別天體相對於質心(質量中心)的距離與自身質量成反比。因此當計算兩個天體的運行軌道時，若其中一个天体质量比另一个明顯大很多，可以大質量物體的質量中心取代共同的質心，不僅方便、誤差也很小。

爱因斯坦认为，引力是时空弯曲造成的，因此，他推翻了牛顿的超距作用假设，该假设认为引力的传播是一瞬间完成的。在相对论中，轨道是时空场的测地线，这样得到的轨道和牛顿学说的预测很接近。这两种理论之间的差别是可以测量出来的。人们设计了一些实验来区分这两个理论，在实验能达到的精度范围内，基本上所有的实验结果都符合相对论的结论。一般而言，两者之间的差别很小，除了超强引力场附近和超高速的情况下。爱因斯坦本人于1915年使用广义相对论解释了水星轨道的反常近日点进动现象，这是相对论效应的第一次理论计算验证。但是，对于大多数短时期的计算，人们通常使用牛顿理论的解法，因为它计算简便而且精度足够高。

行星轨道

在一個行星系統內，行星、矮行星、小行星、彗星和空間中的碎片，都以橢圓軌道繞著中心的恆星運轉著。有些以拋物線或雙曲線軌道繞著中心恆星的彗星，則被認為是未受到這顆恆星的重力束縛住，而不是這個行星系統內的天體。迄今，在太陽系發現軌道明確是雙曲線的彗星仅有一例^[1]。在行星系統內，如果一對天體的質量中心是在大質量的天體之內，另一個天體便是跟隨這這個天體的衛星或人造衛星。

由於相互間的引力攝動，太陽系內行星軌道的扁率會間逐漸變動。水星太陽系內最小的行星，軌道有著最大的扁率，在當前這世紀，火星軌道的扁率是第二大的，軌道扁率最小的則是金星和海王星。

當兩個天體互相環繞，近星點是這兩個天體彼此最接近的位置，遠星點則是這兩個天體彼此距離最遠的位置。.

在橢圓軌道上，繞行與被繞行系統的質心將在兩者軌道的一個焦點上，在另一個焦點上則沒有任何物體。當行星接近近星點時，行星的速度將會增加，而在接近遠星點時，行星的速度將會降低。

參見：克卜勒行星運動定律

了解軌道

参看: 牛頓大炮

簡單了解軌道的方法如下：

• 當物體被拋出去時，會向著原先圍繞旋轉的對象掉落。然而，如果速度夠快的話，軌道的彎曲度會使他落在被圍繞物體的前方。


• 一種力量，像是重力，會將在直線上飛行的物體拉入彎曲的路徑上。


• 當物體掉落時，如果速度夠快（有足夠的切線速度），便會脫離原先的軌道。使用數學分析來理解是非常有用的，因為物體的運動可以在三度空間座標中用相對於質心的一維震盪來描素。

加農炮發射的例子（見下圖），是最常被用來作為行星附近（即地球附近）軌道的說明圖。想像一門被架在高山頂上的加農炮，以平行的方向將砲彈發射出去。如果這座山的高度足以超越大氣層，我們便能忽略空氣對砲彈所產生的阻力（摩擦力）。

如果加农炮以一个较低的初速度发射一枚炮弹，这个炮弹的轨迹将向地面弯曲，并在A点落到地面。当发射的初速度增加时，炮弹在地面上的落点变得更远（如B点），这是因为，在炮弹跌向地面的时候，地面也在远离炮弹（相对第一点）。从技术意义上讲，所有这些运动的轨迹都是“轨道”，它们都是围绕地球引力中心椭圆轨道的一部分，当炮弹接触地面时该轨道被打断。但如果砲彈以足夠快的速度發射，地面的曲度和砲彈落下的彈道弧度相同時，砲彈便在軌道（D）上運行了。像（D）這樣的軌道是圓形的，而如果砲彈發射的速度再增加，軌道便會成為橢圓的（E）或更為橢圓的（F）。當速度增加到所謂的逃逸速度時，軌道便會從橢圓變成為拋物線，砲彈也將飛至無窮遠處不再回來。如果速度更快，軌道將會成為雙曲線。

一旦进入轨道，航天器需要足够高的速度来维持在大气层外。如果一条椭圆轨道延伸到了稠密大气中，该轨道上的航天器就会逐渐降低速度，并再入大气层。有时候，人们会故意使一个航天器进入大气层，这个过程通常被称为大气制动。

牛頓運動定律

在只有兩個物體的系統中，它們只會因為自身的重力相互影響著，它們的軌道能用牛顿运动定律和萬有引力確實的計算。簡單的說，力量的總和就是質量與加速度的乘積，重力正比於質量，而與距離的平方成反比。

在計算上，可以很方便的使用座標系統，將重的物體置於中心（原點），我們可以說輕的物體在軌道上繞著重的物體運轉。
一個靜止不動的物體，在距離大質量物體較遠時的位能，比較近時要高，因為他將向大質量物體掉落下去。
兩個物體的互動，軌道是圓錐曲線，可以是開放（不再返回）或封閉（複回）的軌道，則全看系統動能+位能的總能量。在開放軌道的系統中，在軌道上每一點的速度都會大於在那個點的逃逸速度，而再封閉軌道上每一個點的速度都會低於逃逸速度。

一個開放軌道的形狀是雙曲線（當軌道速度大於逃逸速度）或是拋物線（當軌道速度等於逃逸速度），這兩個物體在軌道上會先彼此接近，當兩個物體到達最接近的距離的前後，軌道開始彎曲，然後兩個物體再彼此遠離。一些來自太陽系外的彗星，就是這種軌道。

封閉軌道的形狀是橢圓形，在一些特殊的狀況下，環繞的物體與中心保持等距離，也就是軌道是圓形。換言之，像在軌道上最接近地球的點叫作近地點，當圍繞著另一個不是地球的天體運轉時，最接近的點就可以叫做近星點（近拱點），衛星在軌道上離地球最遠的點叫遠地點(遠星點，也叫做遠拱點）。連結近拱點和遠拱點的線叫做拱點線（line-of-apsides），這是橢圓的主軸，是橢圓內部最長的部份。

在封閉軌道上的天體經過一定的時間後會在重複他的路線，這就是刻卜勒由經驗所獲得的定律，可以使用牛頓定律推導出來。這些公式的描述如下：

轨道运动分析

(参看轨道方程和克卜勒行星運動第一定律）

ar=d2rdt2−r(dθdt)2{displaystyle a_{r}={frac {d^{2}r}{dt^{2}}}-rleft({frac {dtheta }{dt}}right)^{2}}

和

aθ=1rddt(r2dθdt){displaystyle a_{theta }={frac {1}{r}}{frac {d}{dt}}left(r^{2}{frac {dtheta }{dt}}right)}.

因为力是完全径向的，加速度与力成正比，因此横行加速度为0。可以得到,

ddt(r2dθdt)=0{displaystyle {frac {d}{dt}}left(r^{2}{frac {dtheta }{dt}}right)=0}.

积分之后我们得到

r2dθdt=h{displaystyle r^{2}{frac {dtheta }{dt}}=h}

对于任意常数h积分有

dθdt=hr2=hu2{displaystyle {frac {dtheta }{dt}}={h over r^{2}}=hu^{2}}

我们引入辅助变量

u=1r{displaystyle u={1 over r}}.

如果径向加速度的大小为f(r)，则从运动方程的径向部分中消去时间变量，得：

d2udθ2+u=f(1/u)h2u2{displaystyle {frac {d^{2}u}{dtheta ^{2}}}+u={frac {f(1/u)}{h^{2}u^{2}}}}.

牛顿的万有引力定律说明，这个力与距离的平方成反比：

f(1/u)=f(r)=F(r)m=GMr2=GMu2{displaystyle f(1/u)=f(r)={F(r) over m}={GM over r^{2}}=GMu^{2}}

其中G是引力常数, m是轨道天体（行星）质量，M是中心天体（太阳）质量。带入前面的等式我们得到：

d2udθ2+u=GMh2{displaystyle {frac {d^{2}u}{dtheta ^{2}}}+u={frac {GM}{h^{2}}}}.

所以对于引力–，或更一般地，对于任何的平方反比律，等式的右面变成了一个常数，and the equation is seen to be the 调和方程（up to a shift of origin of the dependent variable）。

所以，轨道方程为：

r=1u=h2/GM1+ecos⁡(θ−ϕ)=ℓ1+ecos⁡(θ−ϕ){displaystyle r={frac {1}{u}}={frac {h^{2}/GM}{1+ecos {(theta -phi )}}}={frac {ell }{1+ecos {(theta -phi )}}}},

其中φ和e是任意的积分常数。

ℓ=h2GM=a(1−e2){displaystyle ell ={h^{2} over GM}=a(1-e^{2})}

是半正焦弦，和a是半长轴。这可以视为极坐标（r,θ）中的圆锥曲线的方程。

轨道参数

参看: 轨道根數

对于一般的椭圆轨道，轴的长度、离心率、最小和最大的距离之间的关系为：

半长轴 = (近拱点 +远拱点)/2 = 极半径

近拱点 = 半长轴× (1 - 偏心率) = 最小距离

远拱点 = 半长轴× (1 +偏心率) = 最大距离

轨道周期

参看: 轨道周期

轨道衰变

如果軌道的某一部分進入了大氣層，它的軌道就會因為拖曳而衰變。每一次通過近心點，這個物體就會與大氣摩擦，並且失去能量。每次，物體都是很精確的在動能最大時損失能量，因此軌道的離心率都會降低（更接近圓軌道）。這與擺錘的能量損失會使他在最低點的速度減慢，與最高點的高度降低現象是相似的。在連續不斷的作用下，軌道受大氣影響的路徑一次比一次長，受到的影響也一次比一次明顯。最後，作用的影響變得很大，即使以最大動能也不能繼續維持軌道在受到大氣層拖曳影響的極限之上。當這種情況發生時，物體將迅速的以螺旋形路徑下降並與中心物體交會。

大氣層邊界的變化很大，當太陽極大期時，大氣層會產生拖曳作用的高度與太陽極小期時相差達100公里以上。

有些具有良好傳導性的衛星也會因為地球磁場的拖曳作用而發生軌道衰變。基本上，金屬線切過磁場時，其作用就像發電機一樣。金屬線會將電子由接近真空的一端移動至接近真空的另一端，軌道能量就會在金屬線中轉換成熱。

軌道可以使用火箭馬達在路經中的某一點改變動能而進行人為的改變，這是將化學能或電能轉換成動能。以這些方法可以促進軌道的形狀和指向的改變。

另一種以人為方法影響軌道的方法是使用太陽帆或磁性帆。這種形式的推力除了來自太陽之外，不需要使用火箭或其他形式的能量輸入來推進，因此可以不受限制的使用。可以參考靜星（statite）所提出的這一種使用方法。

在同步軌道上環繞中心運轉的物體也會因為潮汐力產生軌道衰變。在軌道上的物體因為拖曳使主體產生潮汐隆起，並且因為在同步軌道之中的物體運動得比表面上的物體為快，因此隆起物的移動會滯後一個小的角度。隆起物的重力因而會在衛星的主軸上延著運動方向產生一個微小的分量。隆起的近端會使衛星減速得比遠端造成的加速還大，結果使得軌道衰變。反過來說，衛星給了隆起物一個扭矩，並且加速了他的自轉。人造衛星相對於行星來說是太微小了，因此對行星的潮汐效應影響不了軌道，但是在太陽系內有些衛星在這種機制下遭受過潮汐力造成的軌道衰變。火星最內側的衛星弗伯斯是一個最好的例子，在五千萬年內不是將撞擊至火星的表面，就是將被破壞而形成一個環帶。

最後，軌道還會因為重力波的輻射而衰變。這個機制對絕大多數的天體都是極端微弱的，只有在很巨大的質量和加速度的結合下，例如一對密接的黑洞或中子星互繞的情況下，才會顯現出來。

地球轨道

更多细节请参看地球轨道。

• 近地轨道


• 高椭圆轨道


• 地球同步轨道


• 对地静止轨道


• 对地静止转移轨道


• 极轨道


• 太阳同步轨道

重力的測量

重力常數G被測定的值為：

• (6.6742 ± 0.001）× 10⁻¹¹ N·m²/kg²


• (6.6742 ± 0.001) × 10⁻¹¹ m³/（kg·s²）


• (6.6742 ± 0.001) × 10⁻¹¹ (kg/m³)^-1s^-2.

因此這個常數的因次是密度^-1時間^-2，這對應於以下的性質。

距離的定標（包括物體的大小、維持相同的密度）給予相似的軌道，而毋須顧慮到時間：舉個例子，如果距離被減半，質量為八分之一，重力是16分之一，而重力加速度是二分之一，因此軌道周期維持不變。相似的，當一個物體由塔下墬，它落到地面所需的時間，由塔的尺度或地球的尺度測量都是一樣的。

當所有的密度是原來的四倍，若在相同的軌道上，則速度會加倍。

當所有的密度是原來的四倍，但所有的尺寸都減半，軌道還是相同的，有著一樣的軌道速度。

這些性質可以由下面的公式來解釋。

GT2σ=3π(ar)3,{displaystyle GT^{2}sigma =3pi left({frac {a}{r}}right)^{3},}

對一個半長軸為a的橢圓軌道，一個小物體繞著半徑為r，平均密度為σ的球體，T是軌道週期。

在原子學說演化中的角色

當探測原子結構的實驗在20世紀初期進行時，早期的原子圖像在庫侖力而不是重力的約束下被描繪成微型的太陽系。這與電動力學的論述不符，但是承襲這種圖像導出了精力充沛的電子狀態必須被限制在波函數的軌道上，因此模型進一步的導致量子論的發展。

参看

• 航天飞机


• 圆形轨道


• Clarke轨道


• 亚轨道和orbital spaceflights区别


• 椭圆轨道


• 逃逸速度


• 重力


• 重力弹弓


• 霍曼转移轨道


• 双曲线轨道


• 轨道方程


• 轨道周期


• 轨道速度


• 抛物线轨迹


• 弹道

参考

• Abell, Morrison，Wolff，宇宙大爆炸，第5版，1987，Saunders College Publishing

外部链接

• An on-line orbit plotter: http://www.bridgewater.edu/departments/physics/ISAW/PlanetOrbit.html
  


• 
  Orbital Mechanics（Rocket and Space Technology）


• 受不同種類的力作用下的運行規跡 (Java模擬)

查 论 编 軌道   類型 一般 盒狀 · 捕獲軌道 · 圓軌道 · 橢圓軌道 · 高橢圓軌道 · 逃逸軌道 · 死亡軌道 · 雙曲線彈道 · 傾斜軌道 · 無傾斜軌道 · 吻切軌道 · 拋物線彈道 · 泊接軌道 · 同步軌道（半同步軌道 · 次同步軌道） 地心 地球轨道 · 地球同步軌道 · 地球同步轉移軌道 · 地球靜止軌道 · 太陽同步軌道 · 低地球軌道 · 中地球軌道 · 闪电轨道 · 近赤道軌道 · 月球軌道 · 极轨道 其他 火星同步軌道 · 火星靜止軌道 · 暈軌道 · 利薩如軌道 · 月心軌道 · 日心軌道 · 太陽同步軌道   參數 傳統 i{displaystyle i,!} 軌道傾角 · Ω{displaystyle Omega ,!} 升交點黃經 · e{displaystyle e,!} 離心率 · ω{displaystyle omega ,!} 近心點角 · a{displaystyle a,!} 半長軸 · Mo{displaystyle M_{o},!} 曆元的平近點角 其他 v{displaystyle v,} 真近點角 · b{displaystyle b,} 半短軸 · ϵ{displaystyle epsilon ,} 偏心距 · E{displaystyle E,} 偏近點角 · L{displaystyle L,} 平黃經 · l{displaystyle l,} 真黃經 · T{displaystyle T,} 軌道週期   軌道操縱 雙橢圓轉移軌道 · 對地靜止轉移軌道 · 重力助推 · 霍曼轉移軌道 · 軌道傾角改變 · 軌道定相 · 太空會合   航天動力學相關條目 拱點 · 天球座標系統 · Delta-v預算 · 曆元 · 曆書時 · 赤道座標系統 · 重力轉向 · 地面追蹤 · 行星際傳輸網路 · 克卜勒行星運動定律 · 拉格朗日點 · 多體問題 · 轨道速度 · 軌道效應 · 軌道方程式 · 軌道狀態向量 · 攝動 · 順行和逆行 · 比較軌道能量 · 比較相對角動量 軌道列表

1. 
   ^ https://www.space.com/38580-interstellar-object-spotted-comet-asteroid-mystery.html.  缺少或|title=为空 (帮助)